nLab Fierz identity
Context
Spin geometry
spin geometry, string geometry, fivebrane geometry …
Ingredients
Spin geometry
rotation groups in low dimensions:
see also
String geometry
Fivebrane geometry
Ninebrane geometry
Representation theory
geometric representation theory
Ingredients
Definitions
representation, 2-representation, ∞-representation
Geometric representation theory
-
Grothendieck group, lambda-ring, symmetric function, formal group
-
principal bundle, torsor, vector bundle, Atiyah Lie algebroid
-
Eilenberg-Moore category, algebra over an operad, actegory, crossed module
Theorems
Contents
Idea
What are called Fierz identities in physics are the relations that hold between multilinear expression in spinors. For example for all Majorana spinors in Lorentzian spacetime dimension 4,5,7,11, then the following identity holds (example below):
(Here denotes the Majorana conjugate, are a Clifford representations, the “”-signs denotes symmetrization in the spinor components and summation over repeated indices is understood. The details of this are discussed below.)
In D’Auria-Fré-Maina-Regge 82 it was pointed out that all Fierz identities may be understood as expressing the product operation in the representation ring of the spin group (in some given dimension): for denoting isomorphism classes of irreducible spin representations, then, by definition of irreps, their tensor product of representations decomposes again as a direct sum of irreducible representations
with “Clebsch-Gordan coefficients” . These coefficients are effectively the Fierz identities.
For example for Lorentzian dimension 11 with denoting the unique irreducible Majorana spinor representation, then one finds (D’Auria-Fré 82b, section 3) that the symmetric part in the quadruple tensor product of this representation with itself decomposes as a direct sum of irreps as follows
where the symbols refer to Young diagrams canonically labeling representations (details are in example below).
The point is that the expression from above is a spinor quadrilinear which transforms in the vector representation (due to its one free spacetime index). But that vector representation is missing from the direct sum above, meaning that the spinor quadrilinear has vanishing components in this vector representation, hence that this expression vanishes identically.
In terms of cochains on super-Minkowski spacetimes
We discuss Fierz identities as identities among multispinorial elements of the Chevalley-Eilenberg algebra of super-Minkowski spacetime , regarded as the super-translation supersymmetry super Lie algebra. In this form Fierz identities encode cocycles in the supersymmetry super-Lie algebra cohomology, such as those which serve as higher WZW terms characterizing super p-branes. We follow Castellani-D’Auria-Fré 82, section II.8.
Bilinear Fierz identities
Given a fixed real spin representation , then the odd coordinates of the super Minkowski spacetime supermanifold span, by construction, precisely that representation space, and hence so do the spinorial components of the super vielbein form
since in the construction of super differential forms on , the de Rham operator acts on the odd coordinates just formally, by sending the generator to the new generator named .
Therefore we may identify the spin representation with the linear span (over ) of these elements
were the spin group acts on the elements on the right in the defining way (see at geometry of physics – supersymmetry): a spinorial rotation in a plane by an angle acts by
We may build new spin representations from this one by forming multilinear expressions in the super vielbein. For example the elements in of the form
span, as the spacetime index ranges in , a -dimensional real vector space
which still carries a linear action of the spin group, induced from the spin action on the -s:
Of course similarly we obtain elements
which, if they are non-vanishing at all, span the representation
Now observe that we may say all this more abstractly as follows:
-
the elements span the symmetrized tensor product of representations
-
for given , then the elements of the form form a subrepresentation thereof, equivalent to the vector representation
-
hence there is a direct sum decomposition
in the category of representations of the spin group, which expresses the (symmetrized) tensor product of representations of the Majorana spinor representation as a direct sum of skew-symmetrized tensor products of the vector representation.
Indeed this direct sum decomposition is exhaustive:
Proposition
For and a Majorana spinor representation of , then the following identity holds:
Proof
By the discussion there, the Majorana spinor representation is a real sub-representation of a complex Dirac representation . The latter has the special property that
-
the Clifford algebra contains the full matrix algebra;
-
for the Clifford elements have vanishing trace.
The first point implies that there exists coefficients for such that
The second condition then implies that multiplying this expression with and taking the trace projects out the coefficient :
Notice that it is the last step, identifying the trace over with the - component of the matrix , where we use the symmetrization of the spinor tensor product, namely the identity .
Some of the coefficients in prop. may vanish identically. These are the bilinear Fierz identities, of the form
Example
Let . Write or for the Majorana spinor representation of . Then
Proof
Since we know from prop. that the right hand side has to be some direct sum of representations of the form , it is sufficient to check that there is only one choice of sum such that dimensions match on both sides of the equation.
Now the dimension of is that of the space of symmetric matrices:
while the dimension of is the binomial coefficient
Hence the claim follows from the fact that
Quadrilinear Fierz identities
Now we consider the direct sum decomposition of the tensor product of representations of four copies of a spin representation. This yields the quadrilinear Fierz identities.
Example
The group has rank 5, and hence its irreducible vector representations are labeled by Young diagrams consisting of five rows. For instance
denotes the representation whose elements may be identified with tensors of the form
which are
-
skew-symmetric in indices in the same column;
-
symmetric and trace-less in indices in the same row.
Write again for the Majorana spinor representation. Then the following identity holds in the representation ring:
Proof
As before, this is supposed to follow already by matching total dimensions on both sides
More in detail we have the following decompositions, in the notation from above.
Here for instance the symbol denotes the projection of the term on the left into the direct summand given by the representation of dimension . Similarly:
and some more.
As a corollary:
Example
For then
-
the following Fierz identity holds:
(this is the cocycle condition for the higher WZW term of the M2-brane (Bergshoeff-Sezgin-Townsend 87), AETW 87)
-
the following Fierz identity holds:
(this is the cocycle condition for the higher WZW term of the M5-brane (BLNPST 97, FSS 15)).
(D’Auria & Fré 1982b (3.13) and (3.28); Naito, Osada & Fukui 1986, (2.27) and (2.28))
Proof
The first identity is the result of equation (2) after tracing over the indices and . Under this trace both summands on the right of (2) vanish: because it is trace-free in indices in a column, and because it is skew-symmetric in all indices.
The second identity follows from taking the trace over the indices in (4) and of skew-symmetrizing over all indices in (3). By the symmetry properties of the tensors on the right of both equations, in both cases all tensors vanish except, in both cases, the contribution proportional to , which both identities share. So it only remains to check that the proportionality factor is 3, as claimed. By writing out the skew-symmetrization in the last term in (4) one finds:
where we used that is already skew-symmetric in all indices.
Example
On D=5 N = 2 super Minkowski spacetime (5d supergravity) there are quadrilinear Fierz identities of this form:
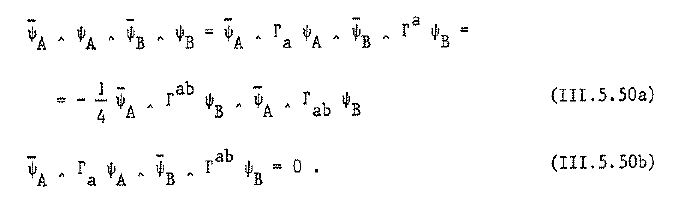
Related concepts
References
Named after Markus Fierz.
The interpretation of Fierz identities as relations satisfied by Clebsch-Gordan coefficients in the representation ring of the spin group originates in
- Riccardo D'Auria, Pietro Fré, E. Maina, Tullio Regge, A New Group Theoretical Technique for the Analysis of Bianchi Identities and Its Application to the Auxiliary Field Problem of Supergravity, Annals Phys. 139 (1982) 93 [doi:10.1016/0003-4916(82)90007-0, spire:167640]
where it was applied to (relevant in D=5 supergravity).
By this method the Fierz identities for (relevant in heterotic supergravity and type II supergravity) are discussed in
- Riccardo D'Auria, Pietro Fré, Geometric Structure of and Super Yang-Mills Theory, Nucl. Phys. B 196 (1982) 205 [inspire:167639]
see also appendix C of
- José Figueroa-O'Farrill, Emily Hackett-Jones, George Moutsopoulos, The Killing superalgebra of ten-dimensional supergravity backgrounds, Class.Quant.Grav.24:3291-3308,2007 (arXiv:hep-th/0703192)
and the Fierz identities for (relevant in 11-dimensional supergravity) were tabulated in
- Riccardo D'Auria, Pietro Fré, Geometric Supergravity in D=11 and its hidden supergroup, Nuclear Physics B 201 (1982) 101-140 [doi:10.1016/0550-3213(82)90376-5, errata]
see also
- S. Naito, K. Osada, T. Fukui, Fierz Identities and Invariance of Eleven-dimensional Supergravity Action, Phys. Rev. D 34 (1986) 536-552 [spire:236376, doi:10.1103/PhysRevD.34.536]
A textbook account of the representation ring method and summary of these results is in
- Leonardo Castellani, Riccardo D'Auria, Pietro Fré, chapter II.8 of: Supergravity and Superstrings - A Geometric Perspective, World Scientific (1991) [doi:10.1142/0224, ch II.8: pdf]
See also:
-
C. C. Nishi, Simple derivation of general Fierz-type identities, Am. J. Phys. 73 (2005) 1160-1163 [arXiv:hep-ph/0412245]
-
Calin Lazaroiu, Elena-Mirela Babalic, Ioana-Alexandra Coman, The geometric algebra of Fierz identities in arbitrary dimensions and signatures, JHEP09(2013)156 (arXiv:1304.4403)
-
Elena-Mirela Babalic, Ioana-Alexandra Coman, Calin Lazaroiu, A unified approach to Fierz identities, AIP Conf. Proc. 1564, 57 (2013) (arxiv:1303.1575)
From the point of view of division algebras and supersymmetry the Fierz identities that give the vanishing of trilinear and of quadratic terms in spinors in certain dimensions are discussed in
- John Huerta, section 2.4 Division Algebras, Supersymmetry and Higher Gauge Theory (arXiv:1106.3385)
The recognition of some Fierz identities as cocycle conditions defining the higher WZW terms of the super p-branes is due to
-
Marc Henneaux, Luca Mezincescu, A Sigma Model Interpretation of Green-Schwarz Covariant Superstring Action, Phys.Lett. B152 (1985) 340 (web)
-
Eric Bergshoeff, Ergin Sezgin, Paul Townsend, Supermembranes and eleven dimensional supergravity, Phys.Lett. B189 (1987) 75-78, In Mike Duff, (ed.), The World in Eleven Dimensions 69-72 (pdf, spire)
-
Anna Achúcarro, Jonathan Evans, Paul Townsend, David Wiltshire, Super -Branes, Phys. Lett. B 198 (1987) 441 (spire)
-
Igor Bandos, Kurt Lechner, Alexei Nurmagambetov, Paolo Pasti, Dmitri Sorokin, Mario Tonin, Covariant Action for the Super-Five-Brane of M-Theory, Phys. Rev. Lett. 78 (1997) 4332-4334 (arXiv:hep-th/9701149)
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber, The WZW term of the M5-brane and differential cohomotopy, J. Math. Phys. 56, 102301 (2015) (arXiv:1506.07557)
Last revised on June 25, 2024 at 14:45:52. See the history of this page for a list of all contributions to it.